我们很常遇到这么一类问题:给出地图,问从起点A到终点B的最短路径.图论里有好几种解决这类问题的算法,比如说Dijkstra算法,它是一种退化的A*算法(h永远为0),每次取g最小的结点进行扩展,为了提高算法的效率,你可以使用最小堆.

但是,有的时候,我们会遇到一类看起来简单得多的问题:地图分为m行n列,从左上角到右下角最短路径有几种走法.

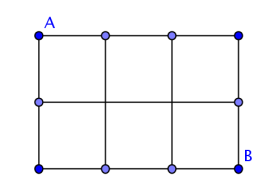
这其实是组合学中最最基础的入门例子,因为要求路径最短,所以我们只能向右走,或者向下走,向右需要走n+1步,向下需要走m步,一共需要走m+n+1步.向右走和向下走的次序即便被打乱,我们仍旧一定能够以最少的步数走到终点,因此只要从m+n+1步中选出n+1步向右走,向下的m步就被确定了.所以,最短路径的走法一共有C(m+n+1,n)种.

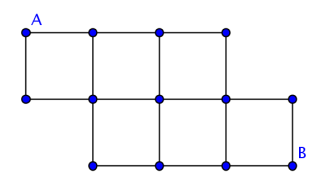
当然,这是假定地图m行n列是对齐的条件下得出的结论.下图中,根据前面的结论,从A到B的最短路径一共有C(2+3+1,2)=15种走法,而实际上,走法只有13种.请仔细思考,为什么组合论的方法在这里会失效呢?(答案见文末)

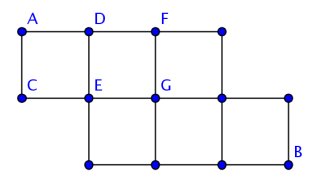
下面给出一种不同于组合论的方法.如下图所示,从A出发到结点C和D,F的走法为1.从A到E的最少步数走法有2种:A->C->E或者A->D->E.从A到G的最少步数走法有3种:A->D->F->G,A->C->E->G,A->D->E->G,注意到2=1+1,3=2+1,你会否有种下意识的觉悟.多年的数学学习告诉我们,由数学归纳法知,记从结点A到结点t最少步数走法有f(t)种,令t的正上方结点和正左方结点分别为t1,t2,则f(t)=f(t1)+f(t2).

当t1不存在时,f(t1)=0,t2同理;为了看得更具体一些,不妨画出示意图如下:

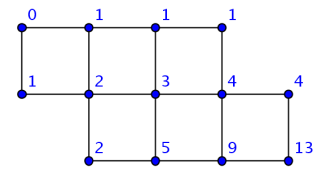
这里的递推思维看起来很简单,其实它是很巧妙的.为了求得某一状态,先求出该状态的所有前驱状态,由状态之间的转化关系求得最终结果.如果你觉得你还没有掌握其中的想法,也许你可以自己画出一些奇形怪状的地图,然后按照递推的思维进行求解.

最后,给出一道题目:

[题目] Arthur要上楼梯,楼梯一共有15阶,Arthur每次可以走1阶或者2阶,问他一共有多少种走法.

[分析] 什么都不说了,直接给答案: f(n)=f(n-1)+f(n-2)

PS: 上面为什么组合论的方法失效呢?因为组合论在故规则的地图里出现了重复状态.