原文:Using Tries 作者:luison9999

翻译 Arthur1989@sysu

Introduction

在文本中索引和搜索一段字符有很多种算法和数据结构,某些被包含在标准库中,但有些并没有.数据结构trie就是这么一个未被包含在标准库中的很好的例子.

以word表示一个字符串,dictionary表示word的集合.在已经有了一个dictionary的情况下,当我们想知道一个特定的word是否在dictionary中时,trie数据结构可以帮上大忙.但是,也许你会问,"既然set和哈希表已经能够实现这一查询了,为什么还需要trie呢?"下面是两个主要的理由:

• trie插入和查询字符串的时间复杂度是O(L)(L表示一个特定字符串的长度).这比起set可要快上不少,即便和哈希表比较,trie还是稍微更快的.
• set和哈希表只支持在dictionary中查找到希望查询的字符串完全匹配的字符串;而trie允许我们容错查找,比如说,字符不一致,共同前缀,字符丢失等等.

trie不仅在TopCoder类型的比赛中很实用,它在软件项目中也有相当多的实际应用.举个例子,考虑一下网络浏览器.你知道浏览器是如何根据已输入的文字自动填充或者给出给出候选输入的吗?是的,通过trie你可以轻易地实现这个功能.你知道拼写检查器是怎么知道你所输入的每一个单词是否在词典中的吗?答案还是一样的,通过trie.你同样可以通过trie,判断输入的单词是否在词典中存在,如果不存在的话给出一个改正的建议单词.

What's a Tree?

可能你早就知道trie的强大了,但是也许你并不清楚trie究竟是什么,它为什么被命名为trie呢?其实,trie的名字是"retrieval"的中缀,因为trie可以通过前缀在词典中搜索可能的字符串.trie数据结构主要基于以下的几点想法:

• trie是一棵树,每一结点是一个字母或者是一个前缀.
• 树根表示一个空的字符串(""),根的直接后继结点表示长度为1的前缀,深度为2的结点表示长度为2的前缀,深度为3的结点表示长度为3的前缀,以此类推.换句话说,深度为k的结点表示长度为k的后缀.
• 以v和w表示trie树的两个结点,v为w的直接前驱,那么v的前缀必须是w的前缀.

下图表示了一棵包含单词"tree","trie","algo","assoc","all",和"also"的trie树.

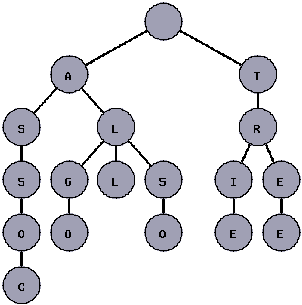
注意,trie树的每一结点并不保存单词完整的前缀或者是单词本身,它仅仅保存一个字母,程序会记下它所有祖先存储的信息.

Coding a Trie

trie树可以通过不同的方法构造,有些方法可以用来在字典中查找与目的字符串略微有些不同的所有其他字符串,但是有些方法仅仅支持完全匹配的查询.本文介绍的是后者.trie的实现将以伪代码的形式给出,因为不同的人使用不同的语言.

我们将实现下面4个功能:

• 插入.该功能允许向词典中插入单词.
• 统计前缀.该功能统计所有以一特定字符串作前缀的单词的数目.
• 统计单词.该功能统计词典中与一给定的字符串完全匹配的单词数目.
• 这里的trie树仅仅支持英文字母表中的字符.

我们打算构造一个struct,用它的数据域来记录结点保存的信息.为了知道与一给定的字符串匹配的单词的数目,每一结点需要有一个变量来表示该结点代表一个完整的单词还是仅仅一个前缀(为简洁起见,给定的单词被认为是一个前缀),它还需要一个变量来统计以给定的单词作为前缀的单词的个数(词典中同一单词可以重复出现),这用一个整形变量就足够了.

正如前面所分析的,每个结点需要一个整形变量prefixes,它表示词典中以该结点代表的前缀为前缀的单词个数.同样,每个结点需要关联到它的所有可能儿子结点(26个关联).理清所有这些细节之后,我们可以知道,struct体需要包含下面的成员:

structure Trie

integer words;
integer prefixes;
reference edges[26];

而且,我们需要实现以下的函数:

initialize(vertex)
addWord(vertex, word);
integer countPrefixes(vertex, prefix);
integer countWords(vertex, word);

首先,以下的代码实现结点信息的初始化:

initialize(vertex)

vertex.words=0
vertex.prefixes=0
for i=0 to 26

edges[i]=NoEdge

addWord函数有两个参数,单词插入所在的结点,插入的单词.当一个字符串string被添加到结点vertex时,我们将根据word的首字母,将它加入相应的vertex的分支,然后将word的首字母去掉.当找不到相应的vertex分支时,我们需要对vertex结点新建一个分支.(Arthur989注:一直递归着这么做下去,直至word为空)所有TopCoder比赛支持的语言都能够在常数时间内删去一个字符串的首元素,而无需拷贝原字符串或者移动字符串的其他元素.

addWord(vertex, word)

if isEmpty(word)
vertex.words=vertex.words+1
else

vertex.prefixes=vertex.prefixes+1
k=firstCharacter(word)
if(notExists(edges[k]))

edges[k]=createEdge()
initialize(edges[k])

cutLeftmostCharacter(word)
addWord(edges[k], word)

函数countWords和countPrefixes是非常相似的.如果(在递归过程中)程序查询的字符串变为空,那么程序只要返回(此时递归所在的)结点所存储的统计变量prefixes就可以了.如果程序查询的字符串非空,我们需要递归查询字符串首字母对应的分支,当分支不存在时,程序将返回0.

countWords(vertex, word)

k=firstCharacter(word)
if isEmpty(word)

return vertex.words

else if notExists(edges[k])

return 0

else

cutLeftmostCharacter(word)
return countWords(edges[k], word);

countPrefixes(vertex, prefix)

k=firstCharacter(prefix)
if isEmpty(word)

return vertex.prefixes

else if notExists(edges[k])

return 0

else

cutLeftmostCharacter(prefix)
return countWords(edges[k], prefix)

Complexity Analysis

通过上文的介绍,你已经感性地知道在trie树中查询和插入一个字符串的复杂度是线性的,但我们却还没着手于具体的分析.在查询和插入的过程中,根据字符串找到下一层对应的儿子是可以在常数时间内实现的,每次程序递归到下一分支时,字符串首字母将被删除;如果字符串长度为L,查询和插入将做L次的递归,因此,这两个操作的时间复杂度为O(L).tire树耗费的内存取决于存储分支的具体方法,以及trie树中有多少单词共享相同的前缀.

Other Kinds of Tries

在我们的介绍中,trie树结点局限于存储小写的英文字母,事实上,它还可以存储其他的信息.我们可以用结点来存储比特或者是字节,此时trie树可以表示任意的数据类型,而不再只是字符串了.发挥你的想像来使用trie树吧!比如说,假设你想在字典中查找一个单词,但是该单词缺失了一个特定的字母,你可以这么修改代码:

countWords(vertex, word, missingLetters)

k=firstCharacter(word)
if isEmpty(word)

return vertex.word

else if notExists(edges[k]) and missingLetters=0

return 0

else if notExists(edges[k])

cutLeftmostCharacter(word)
return countWords(vertex, word, missingLetters-1)
这里我们删去字符串首字母,但不递归查找下一分支.

else

这里我们考虑了两种可能:字符串首字母已被删除和未被删除
r=countWords(vertex, word, missingLetters-1)
cutLeftmostCharacter(word)
r=r+countWords(edges[k], word, missingLetters)
return r

比起原来的程序,修改后的代码的时间复杂度会更高,但是它比检查某一单词的所有子集来得更快.

Problems to Practice

WordFind SRM 232
SearchBox SRM 361
CyclicWords SRM 358
TagalogDictionary SRM 342
JoinedString SRM 302
CmpdWords SRM 268
Scruffle 2007 TCCC Marathon Online Round 1