一点声明
本文译自http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html,
版权归Amit所有.
本文谢绝任意形式的转载,演绎

本文接上一篇 : A*算法中启发函数的使用(1)

栅格地图的启发函数

在栅格上,有很多著名的启发函数可以使用.

曼哈顿距离

标准的启发函数正是曼哈顿距离.不妨看一下你的耗散函数,假设从一个栅格移动到相邻的栅格上的最小代价D.因此,在我的游戏中,启发信息是D倍的曼哈顿距离.

h(n) = D * (abs(n.x-goal.x) + abs(n.y-goal.y))

你应该使用符合你的耗散函数的单位来衡量.

(注:上面的图像中,启发函数可以找到好几条最优路径(下文称之为平局).)

对角线距离

如果你的地图允许对角线移动,那么你需要另外一个启发函数.在直角坐标中,(0,4)到(4,0)的曼哈顿距离是8*D.然而,你本可以简单的将点从(0,4)按东南方向移动至(4,0),所以启发信息应该是4*D.这个函数处理对角线问题,假定直线移动和对角线移动一个栅格的代价都是D:

h(n) = D * max(abs(n.x-goal.x), abs(n.y-goal.y))

如果对角线移动一个栅格的代价并不是D,而是类似于D2=sqrt(2)*D,那么上面的启发函数对你而言又是错误的了.你可以使用一个更为复杂的启发函数代替它.

h_diagonal(n) = min(abs(n.x-goal.x), abs(n.y-goal.y))
h_straight(n) = (abs(n.x-goal.x) + abs(n.y-goal.y))
h(n) = D2 * h_diagonal(n) + D * (h_straight(n) - 2*h_diagonal(n)))

这里我们计算 h_diagonal(n) = 沿着对角线移动的步数, h_straight(n) = 曼哈顿距离,你可以通过考虑所有的对角线移动的步数(每步耗散D2)以及剩下的直线移动的步数(每步耗散D)将这两者结合在一起.

欧几里得距离

如果你的单元可以往任意方向移动(而不是沿着栅格的方向移动),那么你应该使用直线距离:

h(n) = D * sqrt((n.x-goal.x)^2 + (n.y-goal.y)^2)

然而,在这种情况下,由于耗散函数g与启发函数f并不匹配,因此这时A*算法是有问题的.因为欧几里得距离比起曼哈顿距离和对角线距离都更短,你得到的将仍然是最优路径,但A*算法运行时间将更长:

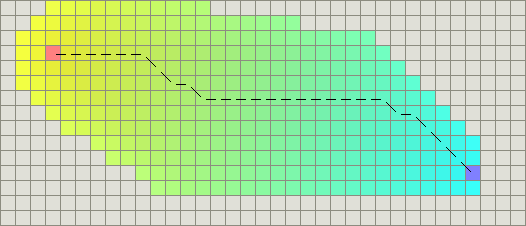
平方的欧几里得距离

在好几个A*算法的网页上,我都看见在欧几里得距离关于避免计算量巨大的开方的计算,方法仅仅是对欧几里得距离做平方.

h(n) = D * ((n.x-goal.x)^2 + (n.y-goal.y)^2)

Do not do this!这绝对会导致g和h的比例的问题.当A*算法计算f(n)=g(n)+h(n)的时候,h的平方会导致它远大于g,这意味着你得到的会是过高估计的启发函数.对于更大的h,这会使得g(n)变得无足轻重了,此时A*算法退化成宽度优先搜索.

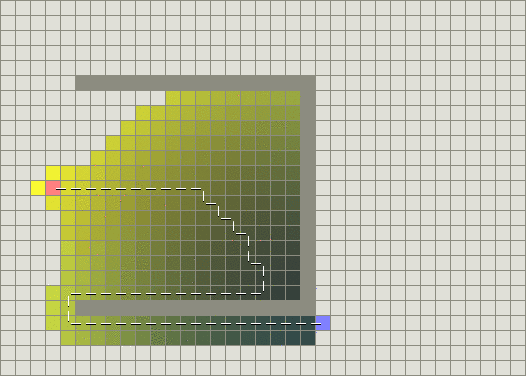
打破平局

在某些地图中,存在着相同耗散值的路径(Arthur1989注:下文中一律称为平局).比如说,在没有凹凸的平原中,使用栅格将会得到许多路径,他们长度是一样的.A*也许会遍历所有的拥有一样的f值的路径,而不是仅仅遍历一条.(如果你的地图中有很多这样的区域,比起A*算法,对于每个栅格的搜索有其他更好的技巧.)

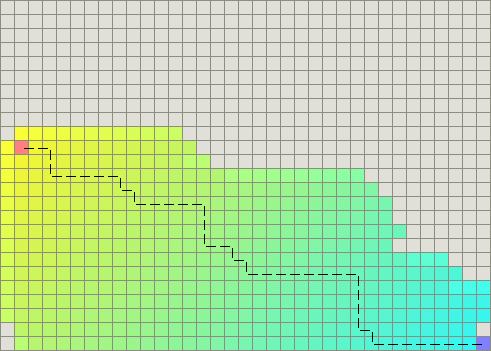
f值相同导致的平局

为了解决这个问题,我们要么可以调整g,要么可以调整h.相对来说,调整h会更加容易.平局的打破对于每个结点的影响必须是确定的(即:它不应该是一个随机数),而且它必须使得每个结点的f值互异.因为A*算法(OPEN表)按结点的f值大小排序,让每个结点的f值互异也就是说,对于有着"相同的"f值的结点,仅有一个会被扩展.

一种打破平局的方法是,稍微的改变h的(单位).如果我们让h的单位减小,(那么h将变大),随着A*算法向目标结点扩展,f值将会增加.不幸的是,这意味着A*算法更偏向于扩展离起始结点较近的结点,而不是扩展离目标结点较近的结点.所以,我们可以将h的单位稍微增大一点(即使是0.1%),此时,A*算法将扩展目标结点旁边的结点.

heuristic *= (1.0 + p)

因子p的选择应该使得 p<(每走一步的最小代价)/(路径的期望最大值).假设你并不希望路径的步数超过1000,你可以将p设定为1/1000.打破平局的微小改变的结果是,A*算法扩展的结点远比原先的算法要少:

在启发信息中改变h或者g的比例

当存在障碍物时,A*算法还是需要找到一条绕过障碍物的路径,但请注意,当绕过障碍物之后,A*算法扩展很少结点:

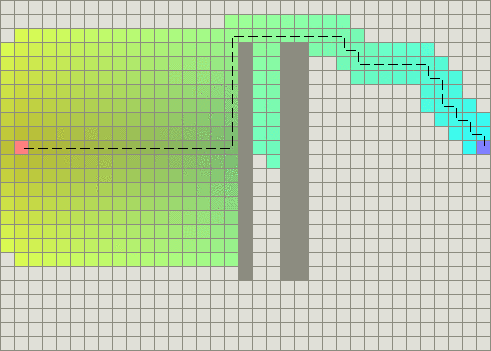
Steven van Dijk 提议了一种更为直接的方法,即把h传递给比较函数.当结点的f值是相同的时候,比较函数可以通过h值判定结点优先级来打破平局.

另外一种打破平局的方法是计算坐标(二维地图中,结点的位置即为笛卡尔坐标)的哈希值,以此来调整启发函数.比起上述调整h的方法,它可以打乱更多的平局.对提出建议的 Cris Fuhrman 致敬.

还有一种不同的打破平局的方法是,偏向于离从起始结点到目标结点的直线较近的路径.

dx1 = current.x - goal.x
dy1 = current.y - goal.y
dx2 = start.x - goal.x
dy2 = start.y - goal.y
cross = abs(dx1*dy2 - dx2*dy1)
heuristic += cross*0.001

上面的代码计算了起始结点到目标结点的向量和当前结点到目标结点的向量的内积.当这些向量不在一队上的时候,内积会变得很大.结果是A*算法稍微的偏向于扩展分布在从起始结点到目标结点的直线附近的结点.当步存在障碍物的时候,A*算法不仅可以扩展更少的结点,它得到的路径看起来也很漂亮.

启发函数中考虑了内积,生成很漂亮的路径

然而,正如上面提过的,当存在障碍物时,A*算法得到的路径看起来会有点奇怪.(注意:路径仍然是最优的)

为了交互地看出这种打破平局的方法带来的效率的提升,你可以查看James Macgill写的A* applet [如果该网址已经不在了,你可以试试 这个镜像].使用"Clear"命令来清空地图,然后在地图的两个角落选中两个结点.当你使用"经典的A*算法"是,你会看见不同结点拥有相同f值的影响.当你使用"Fudge"命令时,你可以看到上面在启发函数中使用内积信息带来的不同.

还有一种打破平局的方法是仔细的构造你的A*算法的优先级队列,它插入一个启发函数值为f的新结点,新结点比原先队列中存在的启发函数值为f的旧结点总是获得更好(坏)的排名.

也许你还可以读读AlphA* algorithm,虽然该算法打破平局的方法更为复杂,但它仍能确保得到的路径是最优的.AlphA*算法是可适应的,而且它应该比上面提到的两种打破平局的方法表现得要更好.但是,后者更为容易实现,因此你可以从后者开始尝试,当需要算法更快时才使用AlphA*算法.

寻找一个区域

如果你想要寻找任何接近于目标结点的区域,你可以构造一个启发函数h'(x),h'(x)是h1(x),h2(x),h3(x),...中的最小值,其中,h1,h2,h3是对于每个临近结点的区域的启发信息.然而,一种更快的方法是,让A*算法查找目标区域的中心结点.