[题目1] 5个人参加网球单打比赛,比赛采用淘汰制,引入轮空制度,问为了决出冠军,一共需要进行几场比赛?

[分析] 这么简单的题目连分析都用不上了,画图如下,红线表示进行了一场比赛,橙色实心圆表示轮空,答案明显是4.

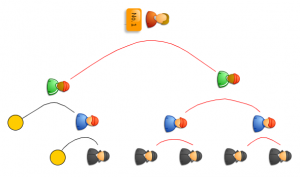[题目2] 当题目中的5人变成79人时,需要进行几场比赛呢?

[分析] 你是否还在画图呢?其实题目1的分析有不弱的诱导性.把参赛队员想成整数,决出冠军可以看作是从79个整数中找出最大值,需要79-1=78次比较,因此答案为78.

上面的两道题目的确是很容易的,现在把题目修改如下:

[题目3] 5个人参加网球单打比赛,比赛采用淘汰制,引入轮空制度,问为了决出冠军,一共需要几次轮空?

[分析] 5不是什么大不了的数字,画图给出得到答案,但是,当将5改成n之后,你还能给出答案吗?其实,这道题在Knuth的名著The Art of Computer Programming中有专章论述.下面给出一种求解方法:

令2^k<n<=2^(k+1),则答案为2^(k+1)-n二进制表示中1的个数.

是不是有点不相信自己的眼睛呢?下面给出证明:

记人数为n时需要的轮空数为f(n),则:

f(2)=0;
当n>2时,

• 如果n为偶数,那么f(n)=f(n/2)
• 如果n为奇数,那么f(n)=1+f((n+1)/2)

将上面两个式子统一为f(n)=s₀+f((n+s₀)/2),n为奇数时,s₀=1;n为偶数时,s₀=0.

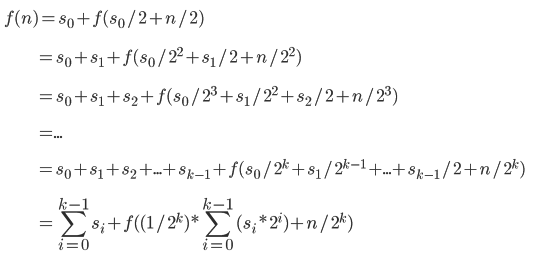
又因为不管n初始为多少,最终会规约到n=2的情况,即式子A:

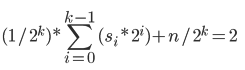
因为f(2)=0,所以有式子B:

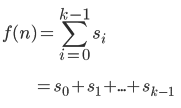
由式子A得式子C:

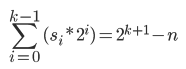
可以看出,式子B的值为式子C 中2的0次幂到k-1次幂的所有系数和,而2的0次幂到k-1次幂之和为2^(k+1)-n,因此式子B的值为2^(k+1)-n二进制表示中1的个数.(请仔细思考!!!)

OK,到此我们已经看到了二进制的能耐了.其实二进制还有很多很多方面的妙用,<Aha!Insight>上有详细的介绍,如果你闲着没事干的话,可以抽出几个钟好好看看.我本想在这里介绍的,可惜这里已经有人写过了.郁闷...

Ps: 悲剧了,wordpress不支持L^AT_EX,画个公式还得转成图片,一不小心还把版式都弄得这么难看..

Ps2: 衡量在三,还是把人家转载文章的链接给出来了,虽然这里也注明了是整理得来的,但是给出原文的真正出处总是最好的.在cn就是这么无奈,随便一篇文章都难找到原作者.

[Update 2009-12-19] 图片设置成初始大小了.